Distributions
Contents
Distributions#
This notebook presents various well-defined numeric probability distributions that frequently arise in statistical analysis.
I have written it to make it easy for you to see different distributions and different parameters. Please play with different values to see what happens!
This notebook also demonstrates how to do some plotting with raw matplotlib.
Math Refresh#
A discrete probability distribution is a distribution over discrete values. These may categorical, ordinal, or numeric. Such a distribution is defined by the probability mass function
A continuous probability distribution is similarly a distribution over continuous values. Because
Such distributions are often defined in terms of a probability density function
The expected value of a random variable is:
For a discrete variable, replace the integral with a sum and the density with the mass:
Mathematically, we denote that a variable follows a distribution with
Probability functions often take parameters that govern their behavior. The number, range, and interpretation of parameters varies greatly from function to function.
Setup#
Let’s load our Python modules:
import numpy as np
import scipy.stats as sps
import seaborn as sns
import matplotlib.pyplot as plt
Functions#
This notebook is going to be much easier to use (and write) if we define some helper functions.
SciPy provides classes that implement many distributions in a compatible interface. We’re going to use those.
Density#
Our first function is going to take a distribution and plot its density. It takes an optional min and max for the
def plot_density(dist, xmin=None, xmax=None, npts=1000, mass=0.9999):
xmin, xmax = find_range(dist, xmin, xmax, mass=mass)
# set up x values
xs = np.linspace(xmin, xmax, npts)
# find corresponding densities
ys = dist.pdf(xs)
# let's start by plotting the mean & median - we plot this first so the density is on top
plt.axvline(dist.median(), linestyle=':', alpha=0.5, label='median')
plt.axvline(dist.mean(), linestyle='--', alpha=0.5, label='mean')
# and plot the density itself
plt.plot(xs, ys)
# and a legend & labels
plt.legend()
plt.xlabel('x')
plt.ylabel('Probability Density')
And plot multiple densities at the same time:
def plot_densities(*dists, xmin=None, xmax=None, npts=1000, mass=0.9999):
ranges = [find_range(d, xmin, xmax, mass) for (l, d) in dists]
xmin = min(r[0] for r in ranges)
xmax = max(r[1] for r in ranges)
# set up x values
xs = np.linspace(xmin, xmax, npts)
# plot y values
for lbl, dist in dists:
# find corresponding densities
ys = dist.pdf(xs)
plt.plot(xs, ys, label=lbl)
# and a legend & labels
plt.legend()
plt.xlabel('x')
plt.ylabel('Probability Density')
Distribution#
We also want to be able to plot CDFs:
def plot_cdf(dist, xmin=None, xmax=None, npts=1000, mass=0.9999):
xmin, xmax = find_range(dist, xmin, xmax, mass=mass)
# set up x values
xs = np.linspace(xmin, xmax, npts)
# find corresponding densities
ys = dist.cdf(xs)
# let's start by plotting the mean & median - we plot this first so the density is on top
plt.axvline(dist.median(), linestyle=':', alpha=0.5, label='median')
plt.axvline(dist.mean(), linestyle='--', alpha=0.5, label='mean')
# and plot the density itself
plt.plot(xs, ys)
# and a legend & labels
plt.legend()
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
Density and CDF#
Let’s also build a way to plot both the density and the CDF at the same time.
def plot_pdf_cdf(dist, xmin=None, xmax=None, npts=1000, mass=0.9999):
xmin, xmax = find_range(dist, xmin, xmax, mass=mass)
# set up x values
xs = np.linspace(xmin, xmax, npts)
# set up 2 plots
fig, axs = plt.subplots(2, sharex=True, figsize=(6,8))
pdf, cdf = axs # extract two axes
# let's start by plotting the mean & median - we plot this first so the density is on top
pdf.axvline(dist.median(), linestyle=':', alpha=0.5, label='median')
cdf.axvline(dist.median(), linestyle=':', alpha=0.5, label='median')
pdf.axvline(dist.mean(), linestyle='--', alpha=0.5, label='mean')
cdf.axvline(dist.mean(), linestyle='--', alpha=0.5, label='mean')
# and plot the density itself
pdf.plot(xs, dist.pdf(xs))
# and the CDF
cdf.plot(xs, dist.cdf(xs))
# and a legend & labels
pdf.legend()
pdf.set_ylabel('Probability Density')
cdf.set_xlabel('x')
cdf.set_ylabel('Cumulative Probability')
Continuous Range#
Now let’s define that find_range function. If we already have xmin and/or xmax, they are left as-is, so we can manually specify the range. But if they are not, we will use the inverse CDF (which SciPy calls the percent point function ppf) to find values such that the specified probability mass will be between xmin and xmax.
Note: in this function, we reassign the parameter variables. Python is call-by-value, so this does not change the underlying values; it simply reassigns our local variables.
Note 2: if we passed a list as a parameter, and modified the list, it would change it for the caller. This is not a violation of call-by-value; rather, it reflects that object references are passed by value. If we modify a list, it is changed because there’s just one list object shared between caller and callee; if we assign the variable to contain a reference to a new list, the caller doesn’t get to see that, because while it has the list object, it doesn’t know anything about the variable in which the function stores a refernce to it. Just something to be careful of.
Anyway, here’s the function:
def find_range(dist, xmin, xmax, mass=0.999):
half_excluded_mass = (1 - mass) / 2
if xmin is None:
xmin = dist.ppf(half_excluded_mass)
if xmax is None:
xmax = dist.ppf(1 - half_excluded_mass)
return xmin, xmax
Mass#
Finally, let’s plot probability mass for discrete distributions:
def plot_mass(dist, xmin=0, xmax=None, mass=0.9999):
if xmax is None:
xmax = dist.ppf(mass + (1 - mass) * 0.5)
# set up x values
xs = np.arange(0, xmax + 1)
# find corresponding densities
ys = dist.pmf(xs)
# let's start by plotting the mean & median - we plot this first so the density is on top
plt.axvline(dist.median(), linestyle=':', alpha=0.5, label='median')
plt.axvline(dist.mean(), linestyle='--', alpha=0.5, label='mean')
# and plot the density itself
plt.bar(xs, ys, width=0.5)
# and a legend & labels
plt.legend()
plt.xlabel('x')
plt.ylabel('Probability')
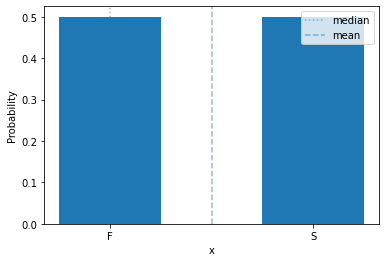
Bernoulli Distribution#
We’ll start with a very simple discrete probability distribution: the Bernoulli distribution.
The binomial distribution is a distribution over two outcomes, such as a coin flip. Conventionally, one outcome is called ‘success’ and the other ‘failure’, because it is used to describe the outcome of a Bernoulli trial, which is an action or even tthat can either succeed or fail.
This distribution has a single parameter,
We often encode success and failure numerically as 1 and 0, respectively.
plot_mass(sps.bernoulli(0.5), 0, 1)
plt.xticks([0,1], ['F', 'S']) # drop excess tick labels & label success & failure
plt.show()
Binomial Distribution#
The binomial distribution is a discrete distribution that describes the number of successes (
The probability mass is distributed like this:
plot_mass(sps.binom(10, 0.5), 0, 10)
plt.show()
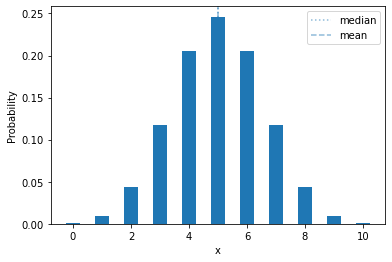
One thing we can immediately note: a fair coin (
If we change the success probability, it shifts left or right:
plot_mass(sps.binom(10, 0.3), 0, 10)
plt.show()
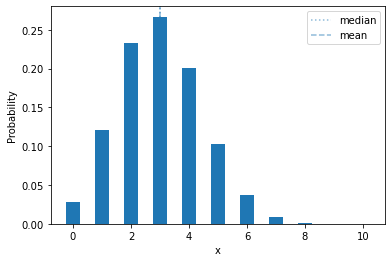
Let’s show a more extreme example:
plot_mass(sps.binom(100, 0.1), 0, 100)
plt.show()
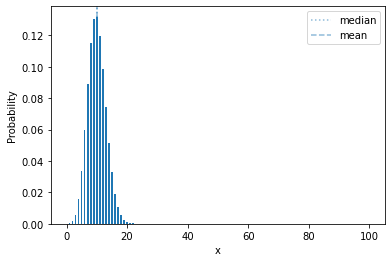
Poisson distribution#
The Poisson distribution frequently shows up when modeling counts. The Poisson has a single parameter, the rate
It is defined by:
Let’s look at one:
plot_mass(sps.poisson(10))
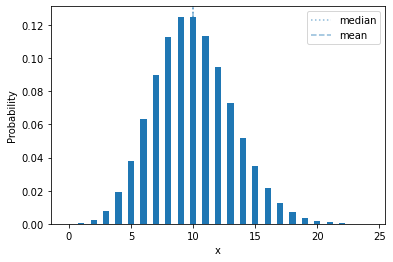
Negative Binomial#
The negative binomial distribution is another distribution that often shows up in counts. It plays a similar role as the Poisson, but has two parameters so that two negative binomials can have the same mean but different variances.
The parameters are
plot_mass(sps.nbinom(10, 0.5))

In terms of a random process, it’s the number of failures you will see if you run a Bernoilli trial with probability
Uniform Distribution#
The uniform distribution distributes its probability mass equally across a range. For a discrete variable, every value has equal mass; for a continuous variable, the entire range has equal density.
In order to be defined, it requires both upper and lower limits to the variable.
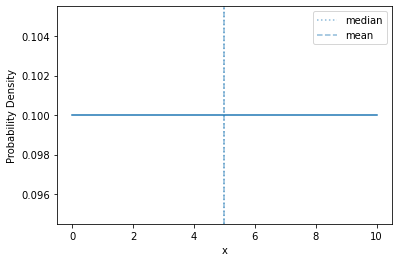
Here’s a continuous uniform density over
plot_density(sps.uniform(0, 10))
And the CDF:
plot_cdf(sps.uniform(0, 10))
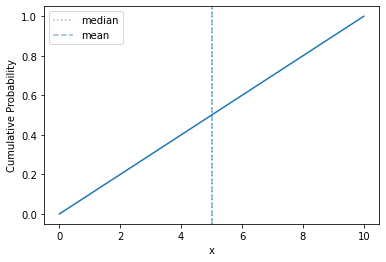
Straight line! About as simple as it gets.
Normal Distribution#
A very common continuous distribution is the normal distribution, also known as the Gaussian distribution and the bell curve. It has two parameters, the mean
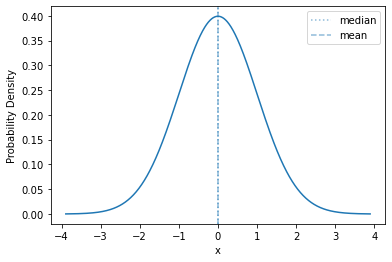
The density of the standard normal (
std_norm = sps.norm()
plot_density(std_norm, mass=0.9999)
And its distribution function:
plot_cdf(std_norm, mass=0.9999)
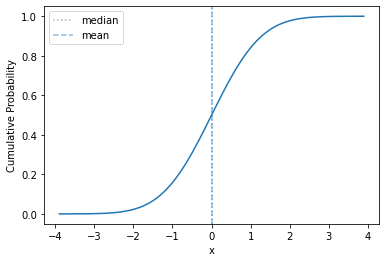
The normal distribution is a location-scale distribution. Such a distribution has location and scale parameters (
If
Let’s see the density of
plot_density(sps.norm(-3, 5), mass=0.9999)

The shape is exactly the same; we have just shifted the mean (to -3) and expanded the range of values (from a standard deviation of 1 to 5). This is what happens with any scale-location distribution!
The normal distribution is unbounded (
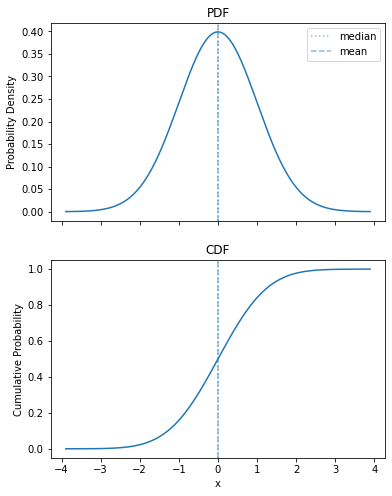
Let’s show off our combined plot, so I can put it in the slide:
plot_pdf_cdf(sps.norm())
Exponential Distribution#
Another common continuous distribution is the exponential. It is a strongly right-skewed distribution over non-negative numbers defined by a rate parameter
Here’s what its density looks like:
plot_density(sps.expon(scale=1))
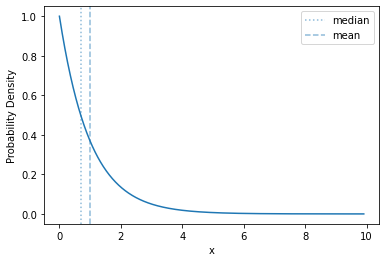
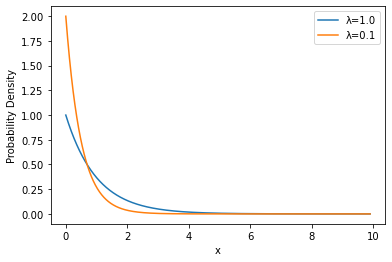
The basic shape of of the exponential distribution does not change as you change the rate - it just rescales the range over which the curve is distributed, and the
plot_density(sps.expon(scale=0.5))

Let’s compare them, directly, though:
plot_densities(('λ=1.0', sps.expon(scale=1.0)), ('λ=0.1', sps.expon(scale=0.5)))
Wrapup#
There are many probability distributions that cover a variety of different processes and models. I have only touched on a few of them here.