Sampling and Testing the Penguins#

This notebook uses the Palmer Penguins data to demonstrate confidence intervals and two-sample hypothesis tests, both using parametric methods and the bootstrap.

Our question: What are the average values of various penguin dimensions (bill length and depth, flipper length, and body mass)? Do these dimensions differ between penguin species?

Setup#

Python modules:

import numpy as np
import pandas as pd
import scipy.stats as sps
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns

Set up a random number generator:

rng = np.random.default_rng(20200913)

Load the Penguin data:

penguins = pd.read_csv('../data/penguins.csv')
penguins.head()
species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex year
0 Adelie Torgersen 39.1 18.7 181.0 3750.0 male 2007
1 Adelie Torgersen 39.5 17.4 186.0 3800.0 female 2007
2 Adelie Torgersen 40.3 18.0 195.0 3250.0 female 2007
3 Adelie Torgersen NaN NaN NaN NaN NaN 2007
4 Adelie Torgersen 36.7 19.3 193.0 3450.0 female 2007

Some of these names are cumbersome to deal with. I’m going to give them shorter names:

penguins.rename(columns={
    'bill_length_mm': 'BillLength',
    'bill_depth_mm': 'BillDepth',
    'flipper_length_mm': 'FlipperLength',
    'body_mass_g': 'Mass'
}, inplace=True)

A few things will be eaiser if we also split out penguins by species:

chinstraps = penguins[penguins['species'] == 'Chinstrap']
chinstraps.head()
species island BillLength BillDepth FlipperLength Mass sex year
276 Chinstrap Dream 46.5 17.9 192.0 3500.0 female 2007
277 Chinstrap Dream 50.0 19.5 196.0 3900.0 male 2007
278 Chinstrap Dream 51.3 19.2 193.0 3650.0 male 2007
279 Chinstrap Dream 45.4 18.7 188.0 3525.0 female 2007
280 Chinstrap Dream 52.7 19.8 197.0 3725.0 male 2007 
adelies = penguins[penguins['species'] == 'Adelie']
gentoos = penguins[penguins['species'] == 'Gentoo']

That’s all we need right now!

Confidence Intervals#

Remember that \(s/\sqrt{n}\) is the standard error of the mean. The SciPy sem function computes the standard error of the mean. We can multiply this by 1.96 to get the distance between the sample mean and the edge of the confidence interval.

So let’s write a function that returns the 95% CI of the mean of some data:

def mean_ci95(xs):
    mean = np.mean(xs)
    err = sps.sem(xs)
    width = 1.96 * err
    return mean - width, mean + width

Warmup: Chinstrap Flippers#

As a warmup, let’s compute confidence intervals for the chinstrap flipper length. We will do this with both the standard error and with the bootstrap.

Let’s get the mean & SD of the Chinstrap penguins:

p_mean = chinstraps['FlipperLength'].mean()
p_std = chinstraps['FlipperLength'].std()  # defaults to sample SD
p_n = len(chinstraps)
p_mean, p_std, p_n

(195.8235294117647, 7.131894258578147, 68)

What’s the confidence interval?

mean_ci95(chinstraps['FlipperLength'])

(194.12838574870136, 197.51867307482803)

Let’s bootstrap the chinstraps, and compute the percentile 95% confidence interval for them:

boot_means = [np.mean(rng.choice(chinstraps['FlipperLength'], p_n)) for i in range(10000)]
np.quantile(boot_means, [0.025, 0.975])

array([194.14705882, 197.5       ])

Let’s break that down a bit. It is a Python list comprehension, a convenient way of assembling a list. It is equivalent to the following code:

boot_means = []
for i in range(10000):
    # compute the bootstrap sample
    boot_samp = rng.choice(chinstraps['FlipperLength'], p_n)
    # compute the mean of the bootstrap sample
    boot_mean = np.mean(boot_samp)
    # add it to our list of bootstrap means
    boot_means.append(boot_mean)

It just does all of that in one convenient line, without excess variables. We then pass it to np.quantile to compute the confidence interval; numpy functions can take lists of numbers as well as arrays.

Now let’s see the distribution of those bootstrap sample means, with a vertical line indicating the observed sample mean:

sns.displot(boot_means, kde=True)
plt.axvline(np.mean(chinstraps['FlipperLength']), color='black')
plt.xlabel('Sample Mean')
plt.ylabel('Density')
plt.show()
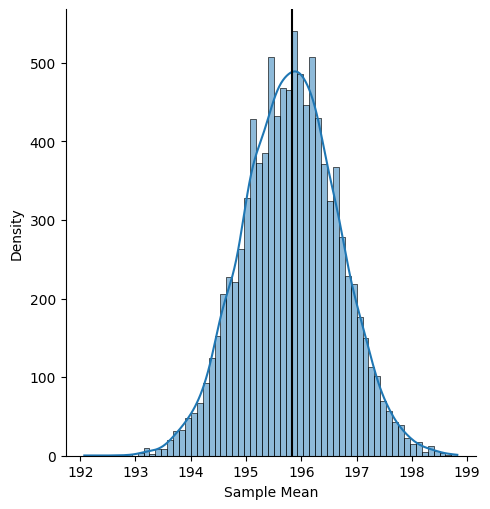
../../../_images/PenguinSamples_23_0.png

We can then compute the confidence interval with the quantiles of this distribution:

np.quantile(boot_means, [0.025, 0.975])

array([194.14705882, 197.5       ])

Penguin Statistics#

With that warmup, let’s look at our various biometrics.

Parametric Estimates#

We’re going to compute CIs for several measurements, but we don’t want to repeat all of our code.

Pandas groupby let us apply a function to each group, which can in turn return a series or a data frame.

Let’s write a function that, given a series of penguin data, returns our statistics:

def mean_estimate(vals):
    # vals is a series of measurements of a single variable
    mean = vals.mean()
    se = vals.sem()  # Pandas has an SEM function too.
    
    ci_width = 1.96 * se
    return pd.Series({
        'mean': mean,
        'std': vals.std(),
        'count': vals.count(),
        'se': vals.sem(),
        'ci_width': ci_width,
        'ci_min': mean - ci_width,
        'ci_max': mean + ci_width
    })

Flipper Length#

Now we can do this to the flipper length:

penguins.groupby('species')['FlipperLength'].apply(mean_estimate).unstack()
mean std count se ci_width ci_min ci_max
species
Adelie 189.953642 6.539457 151.0 0.532173 1.043060 188.910582 190.996702
Chinstrap 195.823529 7.131894 68.0 0.864869 1.695144 194.128386 197.518673
Gentoo 217.186992 6.484976 123.0 0.584731 1.146072 216.040920 218.333064

The confidence intervals don’t overlap. Chinstrap and Adelie are the closest.

Note

The unstack function pivots the innermost level of a hierarchical index to be column labels. Try without it to see what changes!

Bill Length#

penguins.groupby('species')['BillLength'].apply(mean_estimate).unstack()
mean std count se ci_width ci_min ci_max
species
Adelie 38.791391 2.663405 151.0 0.216745 0.424820 38.366571 39.216211
Chinstrap 48.833824 3.339256 68.0 0.404944 0.793691 48.040133 49.627514
Gentoo 47.504878 3.081857 123.0 0.277882 0.544648 46.960230 48.049526

Chinstrap and Gentoo have similar average bill depths - those CIs are very close.

Bill Depth#

penguins.groupby('species')['BillDepth'].apply(mean_estimate).unstack()
mean std count se ci_width ci_min ci_max
species
Adelie 18.346358 1.216650 151.0 0.099010 0.194059 18.152299 18.540416
Chinstrap 18.420588 1.135395 68.0 0.137687 0.269866 18.150722 18.690455
Gentoo 14.982114 0.981220 123.0 0.088474 0.173408 14.808706 15.155522

The bill depth between Chinstrap and Adelie is extremely similar. Gentoo penguins look like they have smaller bills.

Mass#

Finally, let’s look at body mass.

penguins.groupby('species')['Mass'].apply(mean_estimate).unstack()
mean std count se ci_width ci_min ci_max
species
Adelie 3700.662252 458.566126 151.0 37.317582 73.142461 3627.519791 3773.804713
Chinstrap 3733.088235 384.335081 68.0 46.607475 91.350650 3641.737585 3824.438885
Gentoo 5076.016260 504.116237 123.0 45.454630 89.091075 4986.925185 5165.107336

Adelie and Chinstrap are very similar, with Gentoo substantially larger. Look at the CI intervals again!

Bootstrap#

Now we’re going to bootstrap confidence intervals. I’m just going to do it for the flipper length — you should try it for the others!

Let’s take that bootstrap logic from beofre and put it in a function:

def boot_mean_estimate(vals, nboot=10000):
    obs = vals.dropna()  # ignore missing values
    mean = obs.mean()
    n = obs.count()
    
    boot_means = [np.mean(rng.choice(obs, size=n)) for i in range(nboot)]
    ci_low, ci_high = np.quantile(boot_means, [0.025, 0.975])
    return pd.Series({
        'mean': mean,
        'count': n,
        'ci_low': ci_low,
        'ci_high': ci_high
    })

penguins.groupby('species')['FlipperLength'].apply(boot_mean_estimate).unstack()
mean count ci_low ci_high
species
Adelie 189.953642 151.0 188.907285 190.980132
Chinstrap 195.823529 68.0 194.161765 197.500000
Gentoo 217.186992 123.0 216.032520 218.357724

Tip

The apply function also allows us to pass additional named parameters, which are passed directly to the function we are invoking.

penguins.groupby('species')['FlipperLength'].apply(boot_mean_estimate, nboot=5000).unstack()
mean count ci_low ci_high
species
Adelie 189.953642 151.0 188.874172 191.033113
Chinstrap 195.823529 68.0 194.147059 197.500000
Gentoo 217.186992 123.0 216.048780 218.341463

This is the interval Seaborn uses in a catplot of the statistic:

sns.catplot(x='species', y='FlipperLength', data=penguins, kind='bar')

<seaborn.axisgrid.FacetGrid at 0x238b4196f50>

Testing#

Let’s do a t-test for whether the chinstrap and adelie have different flipper lengths. The ttest_ind function does a two-sample T-test:

sps.ttest_ind(adelies['FlipperLength'], chinstraps['FlipperLength'], nan_policy='omit', equal_var=False)

Ttest_indResult(statistic=-5.780384584564813, pvalue=6.049266635901914e-08)

\(p < 0.05\), that’s for sure! The probability of observing mean flipper lengths this different if there is no actual difference is quite low.

Let’s try the bill depth:

sps.ttest_ind(adelies['BillDepth'], chinstraps['BillDepth'], nan_policy='omit')

Ttest_indResult(statistic=-0.4263555696052568, pvalue=0.6702714045724318)

\(p>0.05\). Very. The evidence is not sufficient to reject the null hypothesis that Adelie and Chinstrap penguins have the same bill depth.

Bootstrapped Test#

What about the bootstrap? Remember that to do the bootstrap, we need to resample from the pool of measurements, because the procedure is to take bootstrap samples from the distribution under the null hypothesis, which is that there is no difference between penguins.

We’ll work through it a piece at a time, then define a function.

First, we need to drop the null values from our observations:

obs1 = adelies['FlipperLength'].dropna()
obs2 = chinstraps['FlipperLength'].dropna()

And the lengths:

n1 = len(obs1)
n2 = len(obs2)

And the observed difference in means (since the mean is the statistic we are bootstrapping):

diff_mean = np.mean(obs1) - np.mean(obs2)
diff_mean

-5.869887027658734

Now we’re going to pool together the observations, so we can simulate the null hypothesis (data drawn from the same distribution):

pool = pd.concat([obs1, obs2])
pool

0      181.0
1      186.0
2      195.0
4      193.0
5      190.0
       ...  
339    207.0
340    202.0
341    193.0
342    210.0
343    198.0
Name: FlipperLength, Length: 219, dtype: float64

With the pool, we can now sample bootstrap samples of the means of samples of size \(n_1\) and \(n_2\) from a merged pool:

b1 = np.array([np.mean(rng.choice(pool, size=n1)) for i in range(10000)])
b2 = np.array([np.mean(rng.choice(pool, size=n2)) for i in range(10000)])

We use the list comprehension from before, but this time we wrap its result in np.array to make NumPy arrays that support vectorized computation (lists do not). That then allows us to compute the difference in means for all bootstrap samples in one go:

boot_diffs = b1 - b2
boot_diffs

array([-0.88206077, -0.28632645, -0.25350604, ...,  0.93523568,
       -0.85196728, -0.31077133])

Now, our goal is to compute \(p\), the probability of observing a difference at least as large as diff_mean (in absolute value) under the null hypothesis \(H_0\) (the samples are from the same distribution). So we want to compute the absolute values of the differences, both bootstrapped and observed. NumPy helpfully vectorizes this:

abs_diff_mean = np.abs(diff_mean)
abs_diff_mean

5.869887027658734

abs_boot_diffs = np.abs(boot_diffs)
abs_boot_diffs

array([0.88206077, 0.28632645, 0.25350604, ..., 0.93523568, 0.85196728,
       0.31077133])

And now we can actually compare. The >= operator compares the bootstrapped differences with observed, giving us a logical vector that is True when a bootstrapped difference is at least as large as the observed difference:

boot_exceeds_observed = abs_boot_diffs >= abs_diff_mean
boot_exceeds_observed

array([False, False, False, ..., False, False, False])

Finally, we want to covert this to an estimated \(p\)-value. The np.mean function, when applied to a boolean array, returns the fraction of elements that are True:

np.mean(boot_exceeds_observed)

0.0

No elements were True (if we ran with a much larger bootstrap sample count, we might see a small number of True values). Since our bootstrap sample count estimates the \(p\)-value to approximately 5 decimal places, we conclude that the difference is statistically significant.

Bootstrap Test Function#

Let’s go! We’re going to put all that logic into a short function for easy reuse. Note that variables assigned within a function are local variables: they only have their values within the function, without affecting the global variables of the same name.

def boot_ind(s1, s2, nboot=10000):
    ## we will ignore NAs here
    obs1 = s1.dropna()
    obs2 = s2.dropna()
    n1 = len(obs1)
    n2 = len(obs2)
    
    ## pool the observations together
    pool = pd.concat([obs1, obs2])
    ## grab the observed mean
    md = np.mean(s1) - np.mean(s2)
    
    ## compute our bootstrap samples of the mean under H0
    b1 = np.array([np.mean(rng.choice(pool, size=n1)) for i in range(nboot)])
    b2 = np.array([np.mean(rng.choice(pool, size=n2)) for i in range(nboot)])
    
    ## the P-value is the probability that we observe a difference as large
    ## as we did in the raw data, if the null hypothesis were true
    return md, np.mean(np.abs(b1 - b2) >= np.abs(md))

And with this function, we can compute the bootstrap versions of the tests above:

boot_ind(adelies['FlipperLength'], chinstraps['FlipperLength'])

(-5.869887027658734, 0.0)

The \(p\)-value was very small in the \(t\)-test; it makes sense that we would almost never actually see a mean this large under the null!

Let’s do the bill depth:

boot_ind(adelies['BillDepth'], chinstraps['BillDepth'])

(-0.07423061940007614, 0.6724)

Yeah, those kinds of penguins seem to have the same bill depth.

Conclusion#

We see extremely similar \(p\)-values and confidence intervals for the parameteric methods and the bootstrap. That is expected — if two procedures that claimed to do the same thing returned wildly different results, we would have a problem.

But as we discussed in the videos, the bootstrap works in places where the parametrics won’t.