Overfitting Simulation¶
This notebook demonstrates overfitting, where we learn noise too well.
Setup¶
Load our modules:
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
import scipy.stats as sps
And initialize a random number generator:
rng = np.random.default_rng(20201015)
Simulating Data¶
Let’s define a function to generate n data points. This does three things:
Generates n samples from
randomby 10)Computes
Puts
The function:
def generate(n):
xs = rng.random(n) * 10
ys = xs * 2 + rng.standard_normal(n) * 2
return pd.DataFrame({'X': xs, 'Y': ys})
Now we’re going to define a function to generate polynomials of a varible. For order
def poly_expand(series, order=4):
df = pd.DataFrame({'X': series})
for i in range(2, order+1):
df[f'X{i}'] = series ** i
return df
Now let’s generate our initial data and plot it:
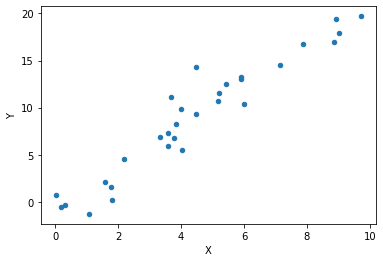
data = generate(30)
data.plot.scatter('X', 'Y')
<matplotlib.axes._subplots.AxesSubplot at 0x165d85a6160>
So far, we’ve been using StatsModels formula interface. That is syntax sugar on top of a lower-level matrix-based interface. For this analysis, we will use that, because it’s easier to programatically set up and manipulate.
The matrix interface requires us to construct an OLS instance with a Y, and a sm.add_constant function does this.
Let’s set it up and fit the model:
X = sm.add_constant(data[['X']])
lin = sm.OLS(data['Y'], X)
lin = lin.fit()
lin.summary()
| Dep. Variable: | Y | R-squared: | 0.919 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.916 |
| Method: | Least Squares | F-statistic: | 317.7 |
| Date: | Fri, 16 Oct 2020 | Prob (F-statistic): | 8.13e-17 |
| Time: | 18:51:19 | Log-Likelihood: | -59.322 |
| No. Observations: | 30 | AIC: | 122.6 |
| Df Residuals: | 28 | BIC: | 125.4 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.7818 | 0.639 | -1.223 | 0.231 | -2.091 | 0.527 |
| X | 2.2016 | 0.124 | 17.824 | 0.000 | 1.949 | 2.455 |
| Omnibus: | 7.323 | Durbin-Watson: | 1.736 |
|---|---|---|---|
| Prob(Omnibus): | 0.026 | Jarque-Bera (JB): | 5.772 |
| Skew: | 0.801 | Prob(JB): | 0.0558 |
| Kurtosis: | 4.431 | Cond. No. | 10.3 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Now let’s fit a 4th-order polynomial model
We’ll this by adding a constant to the poly_expand of the data frame, and fitting the model:
X = sm.add_constant(poly_expand(data['X']))
poly = sm.OLS(data['Y'], X)
poly = poly.fit()
poly.summary()
| Dep. Variable: | Y | R-squared: | 0.938 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.928 |
| Method: | Least Squares | F-statistic: | 94.82 |
| Date: | Fri, 16 Oct 2020 | Prob (F-statistic): | 9.90e-15 |
| Time: | 18:52:06 | Log-Likelihood: | -55.274 |
| No. Observations: | 30 | AIC: | 120.5 |
| Df Residuals: | 25 | BIC: | 127.6 |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -0.1426 | 1.135 | -0.126 | 0.901 | -2.479 | 2.194 |
| X | -1.1816 | 1.803 | -0.655 | 0.518 | -4.896 | 2.532 |
| X2 | 1.7365 | 0.805 | 2.157 | 0.041 | 0.079 | 3.394 |
| X3 | -0.2776 | 0.130 | -2.144 | 0.042 | -0.544 | -0.011 |
| X4 | 0.0138 | 0.007 | 2.027 | 0.053 | -0.000 | 0.028 |
| Omnibus: | 5.714 | Durbin-Watson: | 1.689 |
|---|---|---|---|
| Prob(Omnibus): | 0.057 | Jarque-Bera (JB): | 4.196 |
| Skew: | 0.622 | Prob(JB): | 0.123 |
| Kurtosis: | 4.345 | Cond. No. | 1.98e+04 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.98e+04. This might indicate that there are
strong multicollinearity or other numerical problems.
And now the same with the 10th-order polynomial:
X = sm.add_constant(poly_expand(data['X'], order=10))
poly10 = sm.OLS(data['Y'], X)
poly10 = poly10.fit()
poly10.summary()
| Dep. Variable: | Y | R-squared: | 0.946 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.918 |
| Method: | Least Squares | F-statistic: | 33.49 |
| Date: | Fri, 16 Oct 2020 | Prob (F-statistic): | 5.98e-10 |
| Time: | 18:53:18 | Log-Likelihood: | -53.154 |
| No. Observations: | 30 | AIC: | 128.3 |
| Df Residuals: | 19 | BIC: | 143.7 |
| Df Model: | 10 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.5949 | 2.061 | 0.289 | 0.776 | -3.719 | 4.909 |
| X | -1.1089 | 19.180 | -0.058 | 0.954 | -41.254 | 39.036 |
| X2 | -18.4133 | 51.012 | -0.361 | 0.722 | -125.182 | 88.355 |
| X3 | 35.0879 | 60.911 | 0.576 | 0.571 | -92.401 | 162.577 |
| X4 | -25.8969 | 39.040 | -0.663 | 0.515 | -107.608 | 55.814 |
| X5 | 10.3116 | 14.824 | 0.696 | 0.495 | -20.715 | 41.338 |
| X6 | -2.4437 | 3.495 | -0.699 | 0.493 | -9.759 | 4.872 |
| X7 | 0.3545 | 0.517 | 0.686 | 0.501 | -0.727 | 1.436 |
| X8 | -0.0309 | 0.047 | -0.664 | 0.515 | -0.128 | 0.066 |
| X9 | 0.0015 | 0.002 | 0.636 | 0.532 | -0.003 | 0.006 |
| X10 | -3.017e-05 | 4.97e-05 | -0.607 | 0.551 | -0.000 | 7.39e-05 |
| Omnibus: | 4.482 | Durbin-Watson: | 1.745 |
|---|---|---|---|
| Prob(Omnibus): | 0.106 | Jarque-Bera (JB): | 3.177 |
| Skew: | 0.422 | Prob(JB): | 0.204 |
| Kurtosis: | 4.353 | Cond. No. | 4.80e+11 |
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 4.8e+11. This might indicate that there are
strong multicollinearity or other numerical problems.
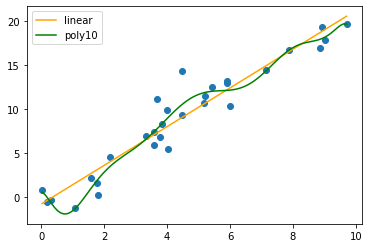
Now let’s plot the data and curves. This time, I’m going to create a linspace, as usual, and then use the fitted model’s predict function to generate the curves (this is easier than manually extracting and writing our own formula):
plt.scatter(data.X, data.Y)
xsp = np.linspace(np.min(data.X), np.max(data.X), 100)
# ysp = poly.predict(sm.add_constant(poly_expand(xsp)))
ysp10 = poly10.predict(sm.add_constant(poly_expand(xsp, order=10)))
ylp = lin.predict(sm.add_constant(xsp))
plt.plot(xsp, ylp, color='orange', label='linear')
# plt.plot(xsp, ysp, color='red', label='poly4')
plt.plot(xsp, ysp10, color='green', label='poly10')
plt.legend()
plt.show()
What are our squared errors on the training data?
np.mean(np.square(lin.resid))
3.0553433680686
np.mean(np.square(poly10.resid))
2.0253086976466195
New Data¶
What about new points from our distribution? Let’s generate some:
test = generate(30)
test['LinP'] = lin.predict(sm.add_constant(test[['X']]))
test['LinErr'] = test['Y'] - test['LinP']
test['Poly10P'] = poly10.predict(sm.add_constant(poly_expand(test.X, 10)))
test['Poly10Err'] = test['Y'] - test['Poly10P']
And compute our test error for each model:
np.mean(np.square(test['LinErr']))
2.992713620832882
np.mean(np.square(test['Poly10Err']))
4.382587964880173
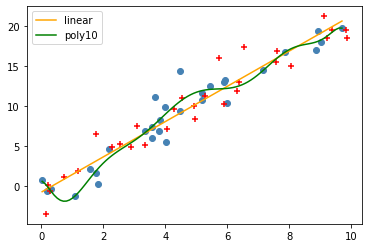
And plot the new points, along wiht the old points and our model:
plt.scatter(data.X, data.Y, color='steelblue')
plt.scatter(test.X, test.Y, color='red', marker='+')
xsp = np.linspace(np.min(data.X), np.max(data.X), 100)
# ysp = poly.predict(sm.add_constant(poly_expand(xsp)))
ysp10 = poly10.predict(sm.add_constant(poly_expand(xsp, order=10)))
ylp = lin.predict(sm.add_constant(xsp))
plt.plot(xsp, ylp, color='orange', label='linear')
# plt.plot(xsp, ysp, color='red', label='poly4')
plt.plot(xsp, ysp10, color='green', label='poly10')
plt.legend()
plt.show()