Tricks with Boolean Series¶
This notebook discusses Boolean series, and various useful things you can do with them.
First let’s import our libraries:
import pandas as pd
import numpy as np
rng = np.random.default_rng(20201103)
Computing Probability¶
If we have a logical series:
xb = pd.Series([True, False, True, True, True, False, False, True, False, True])
xb
0 True
1 False
2 True
3 True
4 True
5 False
6 False
7 True
8 False
9 True
dtype: bool
We can count the number of True values with sum:
xb.sum()
6
We can count the fraction of True values, or the probability of True, with mean():
xb.mean()
0.6
The NumPy equivalents also work:
np.mean(xb)
0.6
Creating with Logical Operations¶
If you do a logical operation (==, <, >, <=, or >=) on a series, comparing it to either a fixed value or another series, you will get a Boolean series.
This is very useful for creating the outcome vector for a logistic regression, as the boolean series will be treated as 1 (True) and 0 (False), and can be predicted with either StatsModels or SciKit-Learn’s logistic regression or other classifier.
For example, if we draw some random numbers:
xs = pd.Series(rng.random(size=1000))
xs
0 0.163352
1 0.333021
2 0.054169
3 0.662442
4 0.517284
...
995 0.882045
996 0.897472
997 0.161948
998 0.850922
999 0.222618
Length: 1000, dtype: float64
xs.hist()
<matplotlib.axes._subplots.AxesSubplot at 0x22e1f5277f0>
xs.describe()
count 1000.000000
mean 0.491382
std 0.285871
min 0.000805
25% 0.235146
50% 0.489305
75% 0.737922
max 0.997661
dtype: float64
We can get a series that is True when the number is at least 0.8:
xs_ge = xs >= 0.8
xs_ge
0 False
1 False
2 False
3 False
4 False
...
995 True
996 True
997 False
998 True
999 False
Length: 1000, dtype: bool
We can verify that values start at 0.8:
xs[xs_ge].min()
0.8050954039782324
Since the values are drawn uniformly in the range
xs_ge.mean()
0.183
Logical Operations¶
The bitwise negation operator, ~, negates a boolean series:
~xb
0 False
1 True
2 False
3 False
4 False
5 True
6 True
7 False
8 True
9 False
dtype: bool
The np.logical_not function also does:
np.logical_not(xb)
0 False
1 True
2 False
3 False
4 False
5 True
6 True
7 False
8 True
9 False
dtype: bool
We can combine them with bitwise and (&) or or (|).
Let’s find all the values between 0.8 and 0.9:
xs_in_range = xs_ge & (xs < 0.9)
xs[xs_in_range].describe()
count 87.000000
mean 0.849424
std 0.028517
min 0.805095
25% 0.826880
50% 0.845260
75% 0.878704
max 0.897472
dtype: float64
We can find everything except
xs_lohi = xs_ge | (xs < 0.2)
xs[xs_lohi].hist()
<matplotlib.axes._subplots.AxesSubplot at 0x22e1edadeb0>
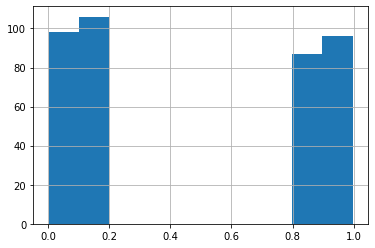
Look, we cut out the middle!